U begin misschien al te duizelen als u het woord ‘priemgetallen’ hoort. Maar ze vormen wel de basisingrediënten voor de getallenleer. Wiskundedocent Filip Moons neemt je mee op wiskundige ontdekkingstocht.
Een getal met eveneel cijfers als inwoners van Australië: dat is, voorlopig althans, het grootst gevonden priemgetal tot nu toe. Het priemgetal bestaande uit 25 miljoen cijfers werd eind 2018 ontdekt door ‘priemjager’ Patrick Laroche en zijn computer. Toch zal ook dit wereldrecord allicht snel van de tabellen verdwijnen. Hoewel het nog steeds een mysterie is waar de priemgetallen zich schuilhouden in de oneindige rij der getallen, weten we wel zeker dat er oneindig veel priemgetallen zijn. Het bewijs dat er oneindig veel priemgetallen zijn, is één van de mooiste en eleganste bewijzen van heel de wiskunde.
Priemgetallen zijn de basisingrediënten van de getallenleer
Priemgetallen zijn getallen die enkel deelbaar zijn door zichzelf en 1. Zo is 7 een priemgetal: enkel deelbaar door 7 en 1. Het getal 6 is geen priemgetal, want het is niet alleen deelbaar door 6 en 1, maar ook door 3 en 2. De eerste 5 priemgetallen zijn 2, 3, 5, 7 en 11. Ga zelf maar verder zoeken en je zal merken dat het steeds lastiger wordt om te bepalen of een getal priem is of niet.
Priemgetallen vormen de basisingrediënten van de getallenleer: elk getal kan namelijk opgeschreven worden als een vermenigvuldiging van priemgetallen. Zo kan pakweg 20 geschreven worden als 20 = 2 x 2 x 5, of 50 kan geschreven worden als 50 = 2 x 5 x 5. Een priemgetal zelf, bv. 19, kan uiteraard niet geschreven worden als een vermenigvuldiging van andere priemgetallen en komt als zo’n vermenigvuldiging gewoon zichzelf tegen 19 = 19.
Voor kleine getallen is het relatief eenvoudig om de priemgetallen te vinden die deel uitmaken van de vermenigvuldiging, maar dat wordt snel een zeer tijdrovende klus als de getallen groter worden. Zo tijdrovend, dat zelfs computers het voor grote getallen niet op een korte tijd berekend krijgen. Daar moeten we eigenlijk blij om zijn, want alle belangrijke online transacties zoals internetbankieren, worden beveiligd op basis van het idee dat getallen allemaal kunnen opgeschreven worden als vermenigvuldiging van priemgetallen, maar dat het voor erg grote getallen verdomd moeilijk is om die priemgetallen snel te vinden.
Er zijn er oneindig veel
Hoewel er nog tal van onopgehelderde mysteries rond priemgetallen hangen, weten we één ding heel zeker: er zijn oneindig veel priemgetallen. Dat weten we al sinds de oude Grieken en het is ook Euclides’ gedachtengang van 2300 jaar geleden waarnaar we je nu meenemen.
Laten we eens uitgaan van het het omgekeerde: er zijn eindig veel priemgetallen. Dan kunnen we die opschrijven op een eindig lijstje. Laten we er bv. van uitgaan dat de eerste 5 priemgetallen de enige priemgetallen zijn, dan krijgen we onze hypothetische “eindige lijst der priemgetallen”: {2, 3, 5, 7, 11}. We maken nu het getal dat, opgeschreven als vermenigvuldiging, bestaat uit alle priemgetallen uit ons lijstje: 2 x 3 x 5 x 7 x 11 = 2310. Met 2310 zijn er geen problemen: we kunnen 2310 probleemloos schrijven als een vermenigvuldiging van priemgetallen. Maar kunnen we geen getallen construeren die wel problematisch zijn, de opvolger van 2310 bijvoorbeeld: 2310 + 1? 2311 kan geschreven worden als:
2311 = 2310 + 1 = 2 x 3 x 5 x 7 x 11 + 1
Hoe zit het nu met 2311 als we het willen opschrijven als een vermenigvuldiging van priemgetallen? Er zijn twee mogelijkheden:
- Ofwel is 2311 zelf een priemgetal. Dat is problematisch, want dan hebben we meteen een priemgetal gevonden dat niet in onze eindige lijst der priemgetallen voorkomt! Onze ” eindige lijst der priemgetallen” zal in dat geval al zeker moeten uitgebreid worden met 2311.
- Ofwel is 2311 geen priemgetal, maar dan moeten we priemgetallen kunnen vinden om 2311 als een vermenigvuldiging van priemgetallen te kunnen opschrijven. Vermits “onze eindige lijst der priemgetallen” slechts uit 5 getallen bestaat, hebben we erg weinig kandidaten: 2, 3, 5, 7, 11. We katapulteren je nu even terug naar de lagere school, de staartdeling: als we 2311 delen door pakweg 5, dan krijgen we:
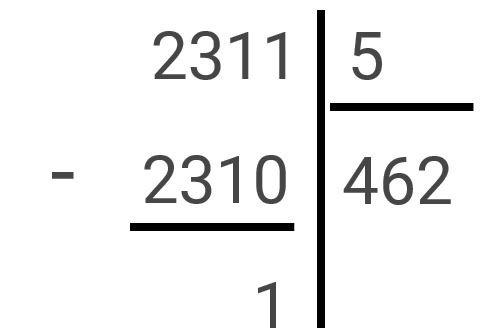
Met andere woorden: 2311 delen door 5 geeft als resultaat 462 met rest 1. 2311 is dus niet deelbaar door 5 (anders is de rest 0). 5 is dus zeker geen kandidaat om in de vermenigvuldiging van priemgetallen van 2311 voor te komen. We kunnen dit nog anders schrijven:
- 2311 = 462 x 5 + 1
Nu is er iets merkwaardig aan de hand: die 462 is niet geheel toevallig de vermenigvuldiging van de andere priemgetallen uit onze lijst: 462 = 2 x 3 x 7 x 11. Als we kijken hoe we aan die 2311 kwamen (2311 = 2 x 3 x 5 x 7 x 11 + 1), is dat ook niet zo verrassend. We hoeven de staartdeling dus niet opnieuw uit te voeren voor de overige priemgetallen: we weten op voorhand dat de deling van 2311 door elk mogelijk ander priemgetal uit onze lijst een rest van 1 zal opleveren. 2311 is dus door geen enkel priemgetal deelbaar uit'”onze eindige lijst der priemgetallen’, geen enkel priemgetal uit onze lijst zal dus voorkomen in de vermenigvuldiging van priemgetallen die 2311 uitkomt. Echter: als 2311 geen priemgetal is, dan moet het wel als een vermenigvuldiging van priemgetallen kunnen geschreven worden! Dat kan dan maar één ding betekenen: er moeten nog andere priemgetallen bestaan dan diegene op ons eindige lijstje.
Uiteraard zijn er meer priemgetallen dan het clubje van 5 op ‘onze eindige lijst der priemgetallen’! Het punt is: ook al maak je een lijstje met miljarden priemgetallen, wat nog steeds een eindig aantal is, als je al die priemgetallen vermenigvuldigt en je past opnieuw het trucje van er 1 bijtellen toe, dan bekom je opnieuw een getal dat ofwel priem is en niet op je eindige lijst stond, ofwel niet-priem is maar niet kan geschreven worden als een vermenigvuldiging van priemgetallen uit jouw eindige lijst. In beide gevallen is je eindige lijst onvolledig en dat zal zo blijven voor elke eindige lijst priemgetallen, waardoor de enige mogelijke conclusie luidt: er zijn er oneindig veel.
Openstaande mysteries
Eén mysterie is vandaag uit de wereld geholpen: er zijn onomstotelijk, oneindig veel priemgetallen. Toch zijn er nog tal van onopgeloste mysteries rond priemgetallen. Zo weten we niet exact waar ze zich schuilhouden: er is nog nooit een sluitend patroon in de priemgetallenrij gevonden. Daarnaast komen priemgetallen vaak in tweelingen voor, waarbij er slechts 1 getal tussen twee priemgetallen zit, bv. 7 en 9, 11 en 13, 17 en 19,… We vermoeden dat er eveneens oneindig veel van zo’n ’tweelingpriemgtallen’ zijn, maar tot op de dag van vandaag is dat slechts een vermoeden: een bewijs vonden we er nog niet voor. Nog een beroemd mysterie is het Vermoeden van Golbach: elk even getal (groter dan 2) kan geschreven worden als de som van twee priemgetallen. Zo is bv. 20 = 17 + 3 of 50 = 31 + 19. Ook hier vermoeden we dat het klopt omdat alle voorbeelden die de mensheid ooit al probeerde, correct bleken, maar ook dat zijn slechts een eindig aantal pogingen: de weg naar wereldfaam ligt open voor diegene die een sluitend bewijs vindt dat het klopt voor alle even getallen.