‘Goed wiskundeonderwijs is géén hogere wiskunde’

We maken ons terecht zorgen over ons (wiskunde)onderwijs. Enkele dagen terug werd in Knack nog maar eens de alarmklok geluid over de dalende onderwijsprestaties. Op 20 jaar tijd gingen we van 33% leerlingen in de topcategorie naar amper 16%, een halvering. Toegang tot wiskundige kennis is een hefboom naar hogere welvaart en economisch succes, zeker voor leerlingen uit kansgroepen. Dat ons wiskundeonderwijs achteruitboert, is een maatschappelijk probleem, dat voornamelijk de zwaksten het hardst treft. Maar hoe nieuw is deze discussie? En waarover hebben we het als we praten over ‘goed’ wiskundeonderwijs? En finaal, hoe keren we het tij? Filip Moons, universitair docent wiskundedidactiek aan de Universiteit Utrecht, kroop in de pen.

Laten we maar met de deur in huis vallen: de discussie over de kwaliteit van ons wiskundeonderwijs is historisch gezien allesbehalve een nieuw debat. Ik kan zo enkele papers openklikken uit de jaren 1920 waarin alarmistisch wordt gedaan over de teloorgang van de wiskundekennis van de jeugd. In het seminale paper ‘The Math Wars’, lijstte Alan Schoenfeld, wereldautoriteit op vlak van wiskundeonderwijs, de verhitte Amerikaanse debatten op.

Nieuw is het debat dus niet, alleen kan met de komst van internationaal vergelijkend onderzoek zoals PISA, de discussie wel iets objectiever gevoerd worden. Ja, Vlaanderen stond in 2003 werkelijk aan de wereldtop op het gebied van wiskunde. Twintig jaar later bevinden we ons in de grijze middenmoot. Maar hoewel het tij nog niet is gekeerd, liggen de kansen voor het grijpen om opnieuw tot de wereldtop door te stoten.

Wat is dat eigenlijk, goed wiskundeonderwijs?

Een eerste belangrijke vraag die antwoord behoeft als we het over ‘goed’ wiskundeonderwijs willen hebben, is wat we eronder verstaan. Jeremy Kilpatrick, een Amerikaans vakdidacticus, kwam rond de milleniumwisseling naar mijn mening het dichtste bij een sluitend antwoord.

Wiskundige bekwaamheid bestaat volgens hem uit vijf componenten.

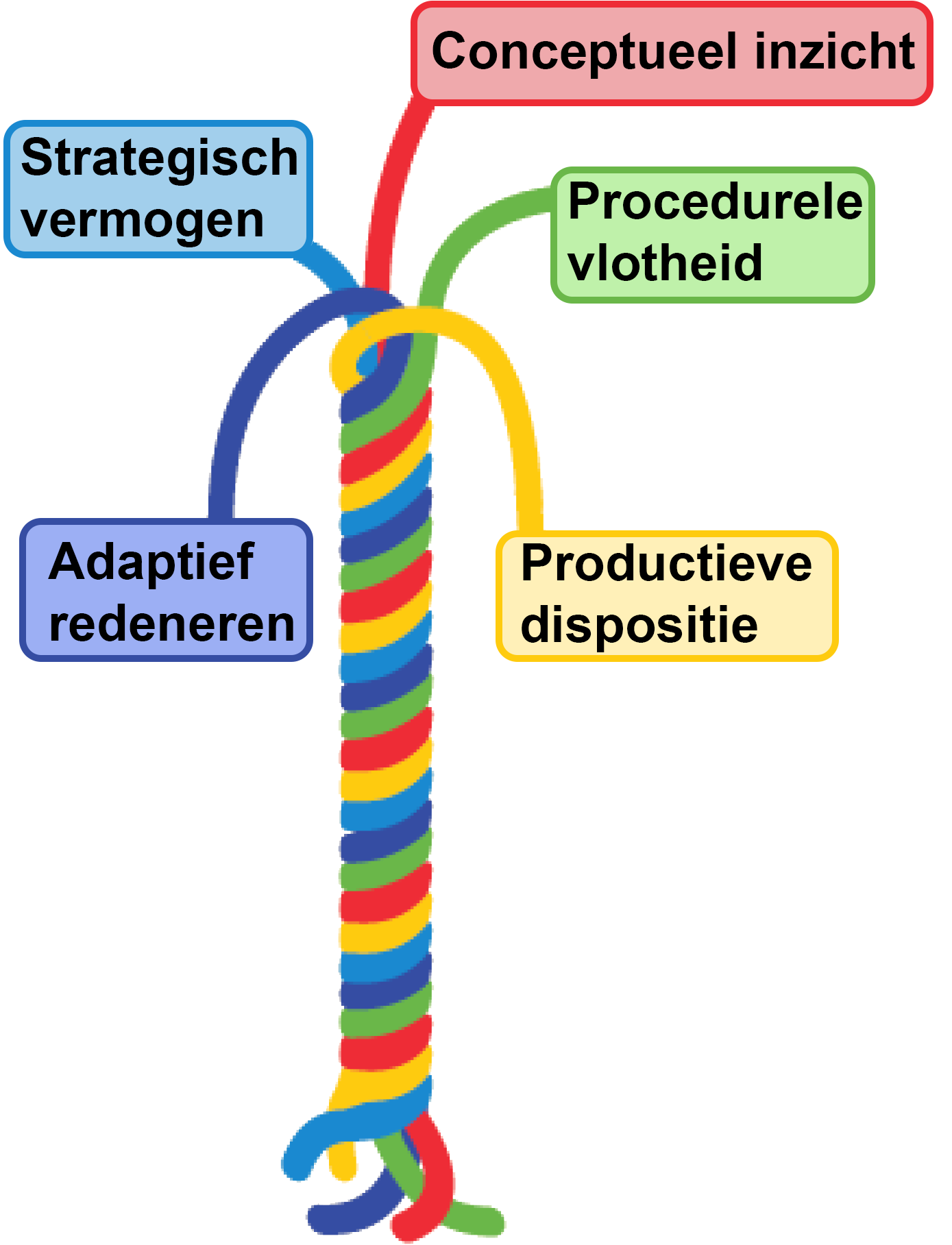
Visueel vormt wiskundige bekwaamheid een draad die kan ontrafeld worden in 5 strengen, wat benadrukt dat de 5 componenten sterk met elkaar verweven zijn. Ik licht ze kort toe:

• Conceptueel inzicht: Begrijpen van wiskundige concepten, operaties en relaties.
  Bijvoorbeeld: Een leerling heeft een rijk inzicht in verhoudingen. Hij ziet meteen in dat als hij 20% korting krijgt, de korting de aankoopprijs gedeeld door 5 is.

• Procedurele vlotheid: Kennis van rekentechnieken om flexibel, accuraat een bepaald type (repetitieve) oefeningen te kunnen oplossen.

Bijvoorbeeld: Een leerling kent zijn maaltafels.

• Strategisch vermogen: Geconfronteerd met een wiskundig probleem, de probleemstelling kunnen vertalen naar het juiste stukje wiskunde.
  Bijvoorbeeld: Een leerling houtbewerking wil 8 kasten maken. De plannen beschrijven echter de benodigdheden voor 3 kasten. De leerling herkent hierin een verhoudingstabel.

• Adaptief redeneren: Vermogen om te reflecteren over een oplossing en een redenering kunnen verklaren.

Bijvoorbeeld: Bij het berekenen van de oppervlakte van een appartement, bekomt een leerling 640m². De leerling komt tot het besluit dat dit toch een uitzonderlijk groot is en zijn oplossing allicht een rekenfout bevat. Hij beslist om alles toch nog eens opnieuw na te rekenen.

• Productieve dispositie: Wiskunde betekenisvol, bruikbaar en de moeite waard vinden, gekoppeld aan de overtuiging dat veel oefenen loont om wiskundig bekwamer te worden.

Merk op dat het één niet zonder het ander kan. Uit de cognitieve psychologie weten we intussen dat leren geen lineair proces is: het is niet zo omdat leerlingen het inzicht in een wiskundig  concept nog niet helemaal scherp hebben, dat er niet kan getraind worden op procedurele vlotheid. Het één versterkt het ander, wat met voldoende herhaling gescheiden in de tijd, tot één omvattend geheel kan leiden.

Afhankelijk van je lesdoel is ook een didactische aanpak meer of minder geschikt. Een leraar die wil aanbrengen dat (a+b)² = a²+2ab+b², doet dat best met de klas te vragen om (8+2)² uit te rekenen. Sommige leerlingen zullen 100 uitkomen (10²), anderen 68 (8²+2²). De verwondering over de twee verschillende uitkomsten is een mooie gelegenheid om leerlingen te laten inzien dat het dubbel product 2*8*2 niet mag vergeten opgeteld te worden, kamp 68 had dus iets over het hoofd gezien. Wil de leraar nadien beginnen met oefeningen maken met (a+b)², dan is voordoen-nadoen zeker een goed idee. Protagonisten van één didactische methode die altijd zou werken, overtuigen me niet: het lesdoel bepaalt de aanpak, niet omgekeerd. Een aanpak die op de klasvloer doorgaans een kladderadatsch is van verschillende pedagogische insteken.

Hoe keren we het tij?

De vraag der vragen: hoe vinden we nu opnieuw aansluiting met de wereldtop? Het is niet dat er de voorbije jaren niets gebeurd is. Met de invoering van de Vlaamse toetsen krijgen scholen de komende jaren elk jaar informatie van de wiskundeprestaties van hun leerlingen. Dat zal vakgroepen ertoe aanzetten om goed na te denken over wat ze in de lestijd wiskunde doen en hoe. Neem bijvoorbeeld de toets probleemoplossend denken, een toets waarop amper 13% van de leerlingen de eindmeet haalt. In die toets worden leerlingen uitgedaagd met vragen waarvan ze niet meteen weten welke wiskunde erachter zit. Die toets zal een brandversneller zijn om het idee op de vloer te laten landen dat ook de streng ‘strategisch vermogen’ aandacht verdient.

Daarnaast stemt het mij alleen maar positief dat vanuit het beleid sterk wordt geduwd op voldoende lestijd voor de basisvakken. De helft van de uren in het basisonderwijs zou naar Nederlands en wiskunde moeten gaan. Ik zou dan ook verwachten dat de eindtermen basisonderwijs focussen op die kernvakken en daar een voldoende kennisrijk curriculum in voorzien. Hopelijk vindt de overheid daar bij de onderwijsverstrekkers een partner.

Daarnaast blijft het essentieel dat er in de lerarenopleiding aan de hogeschool de inhoudelijke lat voor die kernvakken voldoende hoog ligt. Je bepaalt dan misschien niet de instroom, wél de uitstroom. Ook handboeken zouden soms gebaat zijn met wat meer structuur, minder toeters-en-bellen en duidelijkere leerlijnen.

Tot slot: Yes, we can. Goed wiskundeonderwijs is géén hogere wiskunde. Onze leerkrachten kunnen dat waarmaken. Tuurlijk zijn we in staat om van onderwijs terug die emancipatorische motor voor vooruitgang te maken, waarin we iedereen mee krijgen, ook nieuwkomers.  We moeten er alleen wél in geloven en naar handelen!